Pt. 1の続きです.2025/05/20ちょっと改訂
introduction
前回は,超伝導上部臨界磁場Hc2 の温度依存性をWHH理論に基づいて数値計算しました.使用した言語はJulia Lang.です.このWHH理論では,パウリ常磁性効果やスピン-軌道結合の効果を取り入れることができます.これにより,特に低温部分のHc2 curveが変化することを見ました.fittingパラメーターも少ないですし,実験データを解析するときはまずWHH理論を使うのがよさそうです.オッカムの剃刀に従えってわけですね.現実の物質においても,例えばFe(Te, S)超伝導体ではα やλ_SOの寄与が重要となるようです.
しかしながら,WHH理論では実験データをうまくフィットできない場合があるようです.そこで登場するのが,A. Gurevich, "Enhancement of the upper critical field by nonmagnetic impurities in dirty two-gap superconductors", Phys. Rev. B 67, 184515 (2003). によって与えられたモデルとなります.ここでは便宜上,two-band WHHと書きます.タイトルにあるように,超伝導ギャップ(秩序変数)が2成分ある場合の臨界磁場を記述するモデルになっています.マルチバンド超伝導体に適用できそうですね.今回はこのtwo-band WHHに基づいて上部臨界磁場の温度依存性を数値計算してみようと思います.
まず,注目すべき式を見てみます.
ここで,
としました....複雑ですね.超伝導ギャップが2つ存在することから,これらの関係を記述するためには2 x 2行列とその固有値方程式が登場することに由来していそうです.詳しくは論文を参照してください....ムズカシイ...
モデルを理解するため,まずパラメーターに着目しましょう.λ_11, λ_22, λ_12, λ_21, D_1, D_2です.λ_11およびλ_22 はintraband coupling constant, λ_12およびλ_21はinterband coupling constant, D_1およびD_2はdifusivityとなっています.これらを用いてa_1, a_2, a_3, λ_-, λ_0, η が定義されていますね.t は温度T を超伝導転移温度Tcで割った変数です.h は上部臨界磁場Hc2を含む変数で,Dirac定数ℏ,磁束量子Φ_0,Boltzmann定数k_B,真空の透磁率μ_0を用いて定義されます.通常のWHH理論のh とは定義が異なるので注意が必要です.U(x)の中のψ はdigamma関数です.再登場しましたね.two-band WHHは複雑ではありますが,やることは前回と同じです.(1)式を満たすt およびh を探すだけ!
Method
今回もプログラミング言語
Juliaを用いて数値することで,
Hc2の温度依存性を計算します.栗原は実験屋ですが,chat-gptの力を借りて頑張ります.
以下ではJulia 言語で作成したtwo-band WHH Hc2 計算コードを紹介していきます.前回同様,作成環境はJulia 1.9.4,コーディングの際にはJupyter Notebookを用いています.今回もgoogle colab.でコンパイルできることを確認しています.コードへのリンクはこちら.まずはコンパイルの際に必要となるSpecialFunctions, Optim, Plotsパッケージのインポートと,物理定数を定義します.その後,Tcやλ, D を定義します.
h を求めるコードを書くため,(1)の左辺を2乗した関数を新しく定義しました.
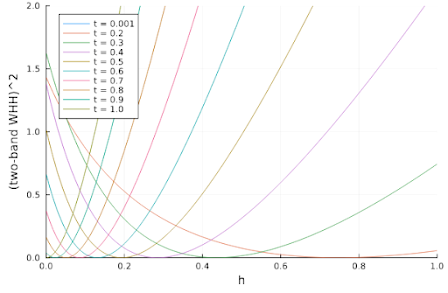
これを(2)式とします.この関数がゼロとなり,かつ最小値となるようなh をまたもや見つけます.直感的にわかりやすいので,今回もいろいろなt における(2)式のh 依存性をグラフにしてみました.
やっぱり最小値を見つければよさそうです!一見すると単純な関数に見えますね.最適化も簡単そう....が,グラフの表示範囲を広げてみるとそう単純ではないことが分かります.
このように,
極小が2か所存在する温度が出てきます.厄介ですね.適当に最適化すると連続した
h-
t カーブにならなそうです.これを回避するコーディングが必要です.注意点はchat-gptが教えてくれました.
なるほど,非線形バリバリ複雑ちゃんな(2)式のOptimを実行する際には,
h の範囲やintervalに気を使えってことですね.
Optimをいろいろな温度t で実行していき,h のt 依存性を得ます.このとき,最初にh = h_1 で(2)式がゼロになり,次にh = h_2 > h_1でもゼロとなった場合には,h_2を最適なh として選択するようなコードとなっています(chat-gptの力).(2)式のt 依存性のグラフをよく見てみると,t = 1のときに h = 0 となるのは h_2となっていることが理由です.転移温度よりも低温でHc2がゼロになることってあるんですかね?それはそれで面白そう.
Result
ここでは例として,two-band WHH理論の論文に記載されているFig. 3を再現してみます.λたちに関してはλ_11 = 0.81, λ_22 = 0.285, λ_12 = 0.119, λ_21 = 0.09で固定し,η = 0.05, 1, 200の3パターンについてHc2を計算します.グラフの描画にはPlotsパッケージを用いています.縦軸はHc2(T )/Hc2(T = 0 K),横軸はt です.結果は以下の通りです.
通常のWHH理論と比べ,低温側でHc2が上昇する,もしくはTc近傍でHc2が急増するのが特徴的です.このように,Fig. 3の結果を再現できました.コードは大丈夫そう,と言いたいのですが,何点かでh の最適化がうまくいっていません.何が原因かを調べるため,Optimのh に関する条件を変えてみたところ,もっとひどくなったり,逆によりよくなったりすることがわかりました.chat-gptさんの言うことは正しかった...このあたりは今後の課題です.
Conclusion
今回紹介したコードによって,通常のWHH理論に加えてtwo-band WHH理論に従うHc2 curveが計算可能となりました.どんどん器用貧乏になるな.コーディングに関してはまだ詰められるところはありますが,実験データのフィッティングに使用するには問題ない程度かなと思います.あとは(3)式およびt = T/Tcを用いることで,Hc2-T グラフが得られるでしょう.しかしパラメーターが多いので大変そう...λ,η,D を最適化するコードも必要ですね...
このコードをベースに解析した結果を学術論文に掲載したり,なにかで使用した場合には,栗原まで一言お知らせ頂ければ幸いです.え?two-band WHHじゃフィットできない?もしかしてdirty limitじゃなくてclean limitのHc2理論が必要なんですか???そんな…






コメント
コメントを投稿