Julia lang.で超伝導上部臨界磁場の理論曲線を計算したい Pt. 1
Introduction
筆者が所属する研究室では,鉄系超伝導体Fe(Te, S)の実験的研究に取り組んでいます.特に2024年度は,大学院生と一緒に物性研究所・国際超強磁場科学研究施設のパルスマグネットを共同利用させていただき,強磁場磁気抵抗測定からFe(Te, S)の臨界磁場を測定しました.いわゆるHc2というやつですね.TeX記法だと$H_\mathrm{c2}$.実験結果からHc2の温度依存性が得られるので,これを理論式でフィットできればいろいろなことがわかります.そして分かったことを論文にまとめてaccept!!!されれば業績となります.音波以外もできるってことを見せなければ...
これまでの理論研究によって,ある温度Tにおける臨界磁場Hc2が満たすべき関係式が与えられています.今回は N. R. Werthamer, E. Helfand, and P. Hohenberg, "Temperature and Purity dependence of the Superconducting Critical Field Hc2. III. Electron Spin and Spin-Orbit Effects", Phys. Rev. 147, 295 (1966).よって与えられた,いわゆるWHH理論を用いて実験データを解析します.このWHH理論では,温度T を超伝導転移温度Tc で割ったt,および臨界磁場を含むh を変数とする以下の関係式を与えています (本当はh の上にバーを付けます.ブログでは入力できないので省略します).
ここでψはdigamma関数と呼ばれる特殊関数です.解析的にHc2を求めるのは困難ですね...なんとかしなければ...
Method
そこでプログラミング言語Juliaを用いて数値することで,Hc2の温度依存性を計算します.実験屋ですが頑張ります.以下ではJulia 言語で作成したWHH Hc2 計算コードを紹介していきます.作成環境はJulia 1.9.4.コーディングの際にはJupyter Notebookを用いています.なにそれ?という方はAIに聞きましょう.PCにインストールするのがめんどくさい方は,google colab.を使いましょう.こちらにコードへのリンクを掲載しておきます.Julia言語を使えるように,「ランライム→ランタイムの変更→ランタイムのタイプをJuliaに設定」が必要です.今回のコーディングの際は,chat-gptにかなり助けてもらいました.最初の数行は,コードの実行に必要となるパッケージのインストールや物理定数を定義しています.digamma関数は,特殊関数を利用するためのSpecialFunctionsパッケージをインストールすれば値を計算できます.
まず,WHHで重要なパラメーターを定義しておきます.パウリ常磁性効果を特徴づけるα (Makiパラメーターと呼ばれる)およびスピン-軌道結合を記述するλ_SOです.また,h とHc2を関係づけるdHc2/dt|(t = 1)も重要です.これらパラメーターは,Notebookの4段落目で入力しています.注意点としては,α, λ_SOの選び方によっては(2)式のγ が定義できなくなる場合があることです.コーディングではこのエラーを避けています,とchat-gptに教えてもらいました.
h を求めるコードを書くため,(1)式を変形した以下の関数に着目しましょう.
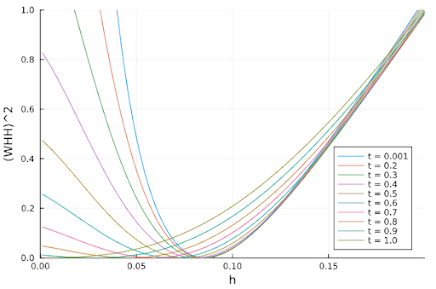
これを(4)式とします.この関数がゼロとなり,かつ最小値となるようなh を見つければよいです.言葉だけだとわかりにくいので,いろいろなt における(4)式のh 依存性をグラフにしてみます.以下の通りです.
グラフを見るとわかりやすいですね.最小値を探せばよいです.超伝導転移温度に対応するt = 1ではh = 0が最小値を与え,t を小さくするとh が大きくなるので,臨界磁場の温度依存性をなんとなく記述できる気がしてきました.ある温度t における(4)式の最小点は,JuliaのOptimパッケージを利用して探します.
Results
Optimをいろいろな温度t で実行していき,h のt 依存性を得ます.ここでは例として,α = 4.5, λ_SO = 0.3の結果を以下に示します.グラフの描画にはPlotsパッケージを用いています.縦軸はHc2(T )/Hc2(T = 0 K)としています.
それっぽいHc2 curveになりましたね.Fe(Te, S)系の上部臨界磁場はα およびλ_SO が有限になっているようです.解析の参考にしよ.Fig. 3のパラメーター依存性を再現できました.コードは大丈夫そう.あとは(3)式およびt = T/Tcを用いることで,Hc2-T グラフが得られます.
今回紹介したコードによってWHH理論に従うHc2 curveを計算可能であることを示せました....示せましたよね...?あとは実験データをフィットするようにα,λ_SO,dHc2/dt|(t = 1)を見つければ解析終了です.あと一歩ですね!...いやここからがスタートです.論文書きます...
今回のコードは素人が書いたものです.最適な書き方などはまったくもって考えておりません.というかわからない...しかしながらたたき台にはなると思いますので,各々が分かりやすく最適な書き方に変えていただければと思います.実験データのフィットに関しても,コーディングで最適なα, λ_SOを見つけるほうがいいかなと思います.が,ダメ.栗原の今後の課題です.
このコードをベースに解析した結果を学術論文に掲載したり,なにかで使用した場合には,栗原まで一言お知らせ頂ければ幸いです.え?フィットできない?もしかしてtwo-band WHH理論が必要なんですか?そんな...
Appendix
α, λ_SOの値によっては,以下のようなh-t グラフになることがあります.
これは最適化がうまくいってないときに起こります.こうなった場合は,(WHH)^2のグラフを見ながら"initial_h_values"の範囲を変えたりしてみてください.




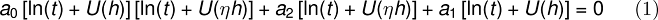

コメント
コメントを投稿